メカトロニクス学の中心である制御工学を学ぶための基礎となる数学を習得することを目的とします。まず、数の概念(整数、実数、有理数、複素数)を復習し、数と図形をつなぐ座標について学びます。つぎに、複素数と2次元平面を対応づけながら複素数の数学的扱いを習得します。さらに、これらをコンピュータを利用して理解する方法を学びます。これらの学習は、制御工学の重要な目的である微分方程式の数値解を得るためのシミュレーション技法などに役立ちます。
工業数学Ⅰ,Ⅱで学べること
本科目を学習することにより問題解決のための手段として数学的スキルが役立つことを理解できます。すなわち、現実問題を数学の世界に写像し(モデリング)数学のツールを使って解を導出し(問題解決)、それを可視化(シミュレーション)し実現(実装)するための実践的方法の基礎を身に着けることができます。この問題解決プロセスは2年次、3年次のモデリング、制御系解析や設計に関する授業、演習、実験で基礎から応用に発展的に展開されます。


本科目を学習することにより問題解決のための手段として数学的スキルが役立つことを理解できます。すなわち、現実問題を数学の世界に写像し(モデリング)数学のツールを使って解を導出し(問題解決)、それを可視化(シミュレーション)し実現(実装)するための実践的方法の基礎を身に着けることができます。この問題解決プロセスは2年次、3年次のモデリング、制御系解析や設計に関する授業、演習、実験で基礎から応用に発展的に展開されます。
カリキュラムについて

受講生は指示された学習内容についてビデオ教材と教科書を使って自宅学習の時間に事前に予習します。教室では学生同士のグループ学習と担当教員やティーチングアシスタントのアドバイスを参考に演習課題に取り組みます。進度の早い学生はグループでの教え合いを進め、受講生全員がこの授業の目的を達成することを目指します。達成状況は中間試験やルーブリックにより逐次自己チェックを行います。
 |
 |
 |
|
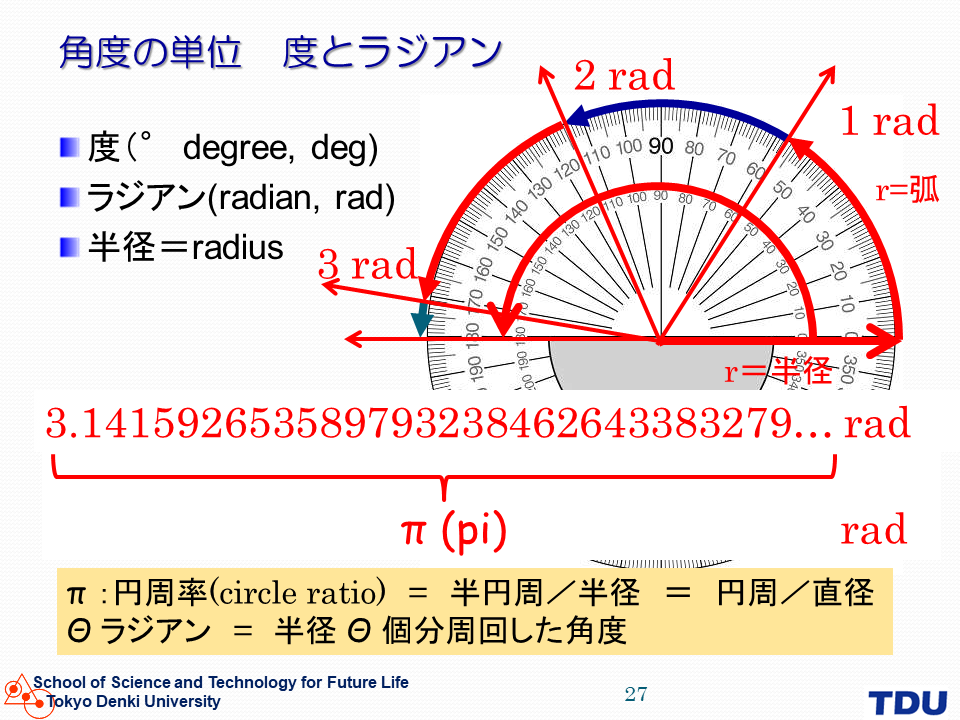
角度1ラジアンの定義をもう一度確認しましょう。 |
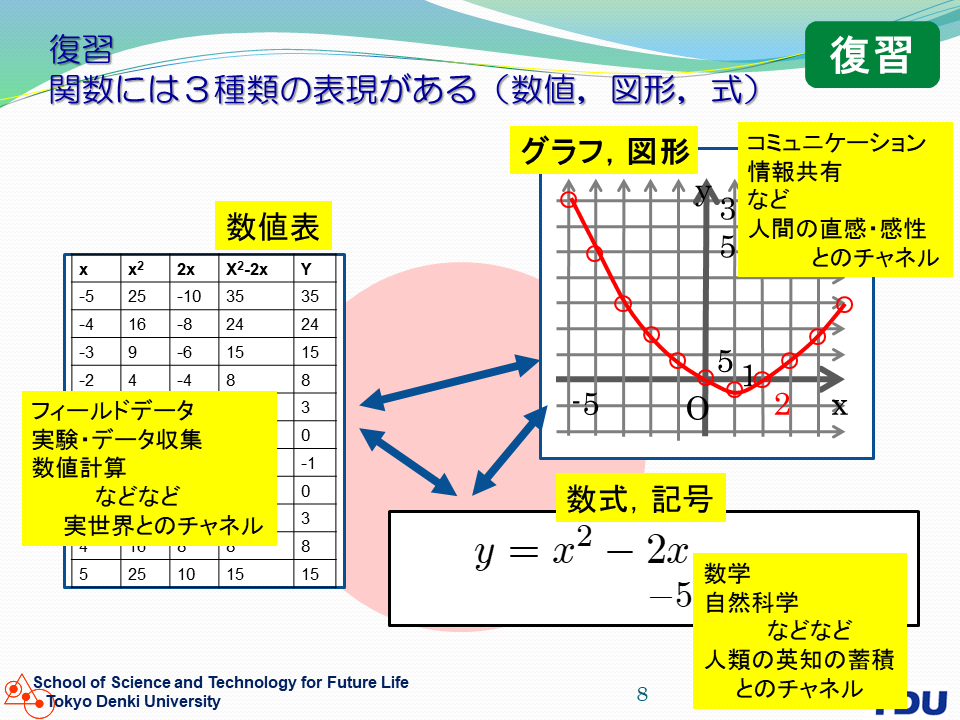
数表とグラフと数式を自在に使いこなせることは語学としての数学の基本スキルです。 |
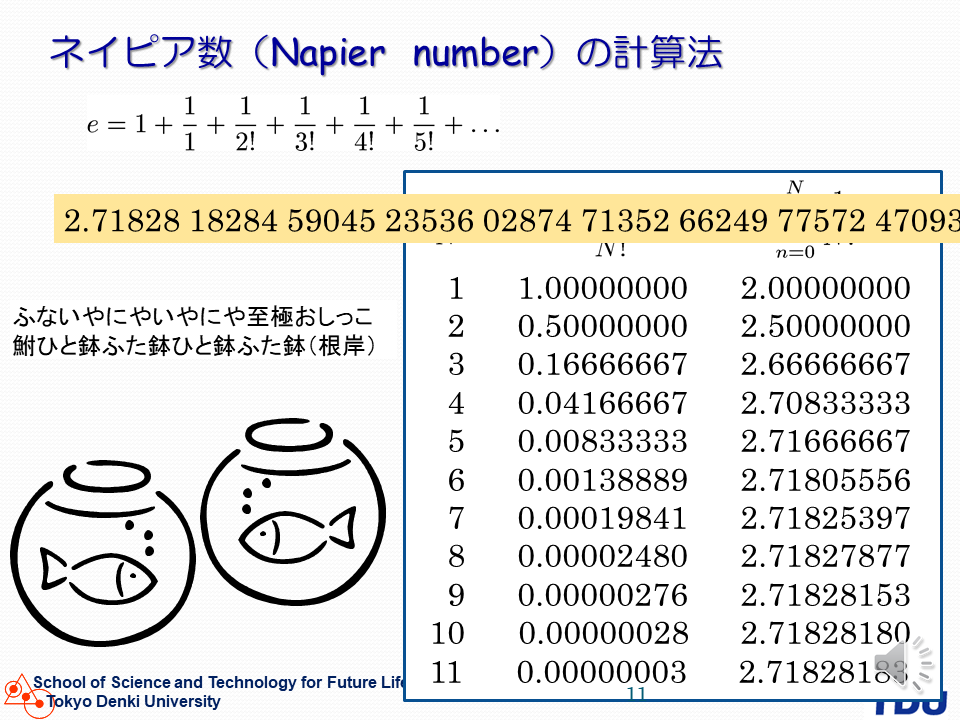
ネイピア数は制御工学や電気工学分野の大事な定数です。 |
 |
 |
 |
|
オイラーの公式は古典制御理論において最も基本となる公式です。 |
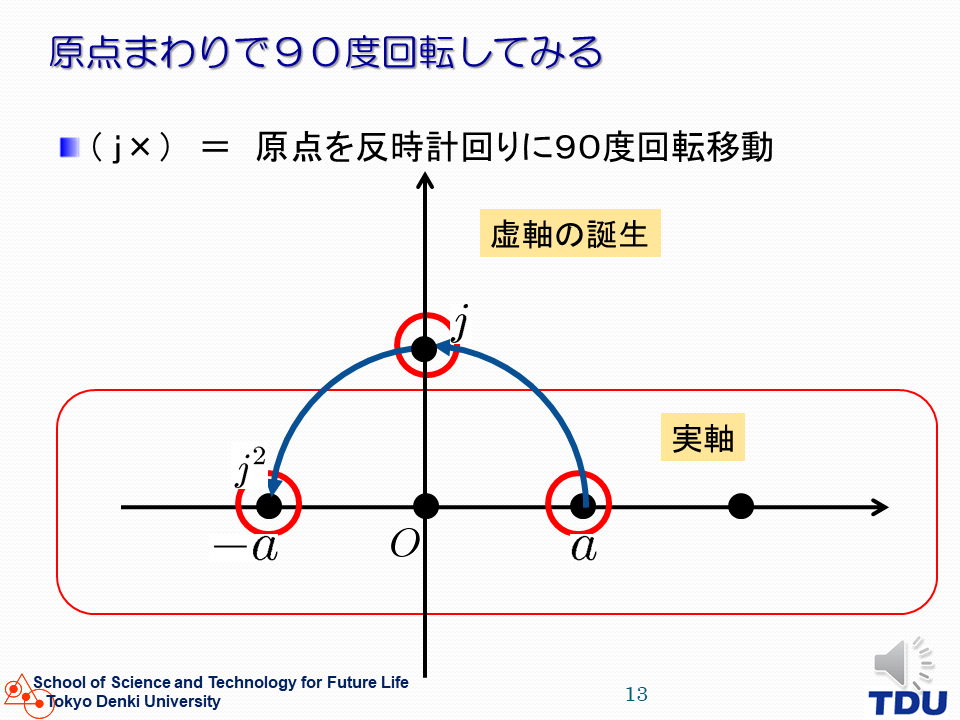
虚数単位 j をかけることは90度の回転操作に対応します。 |
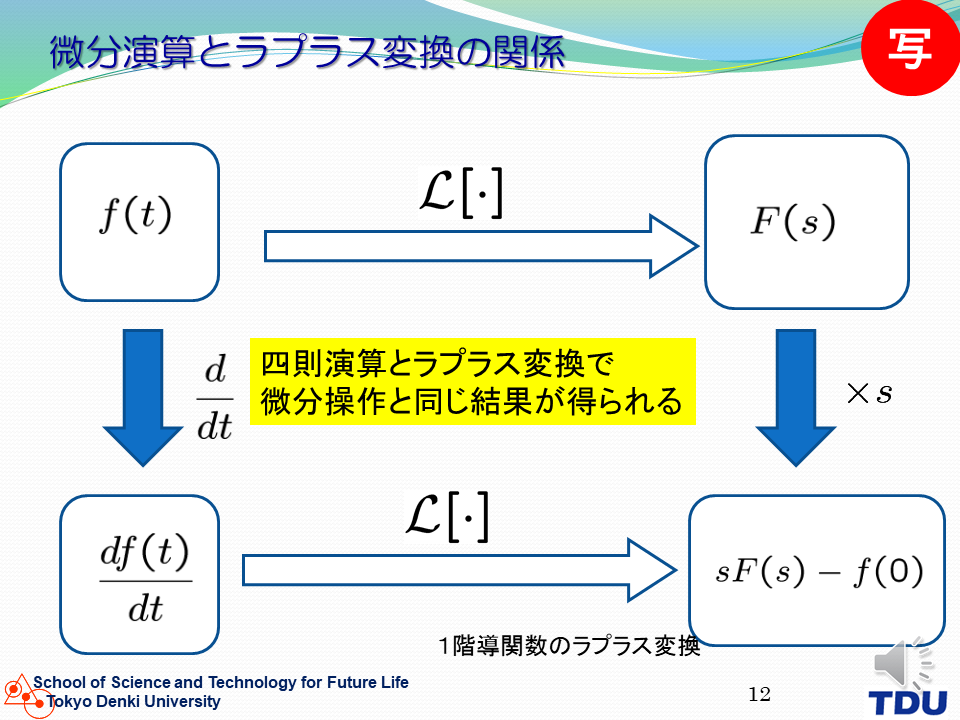
時間領域での微分演算操作は周波数領域でのsの乗算操作に対応する。 |
 |
 |
|
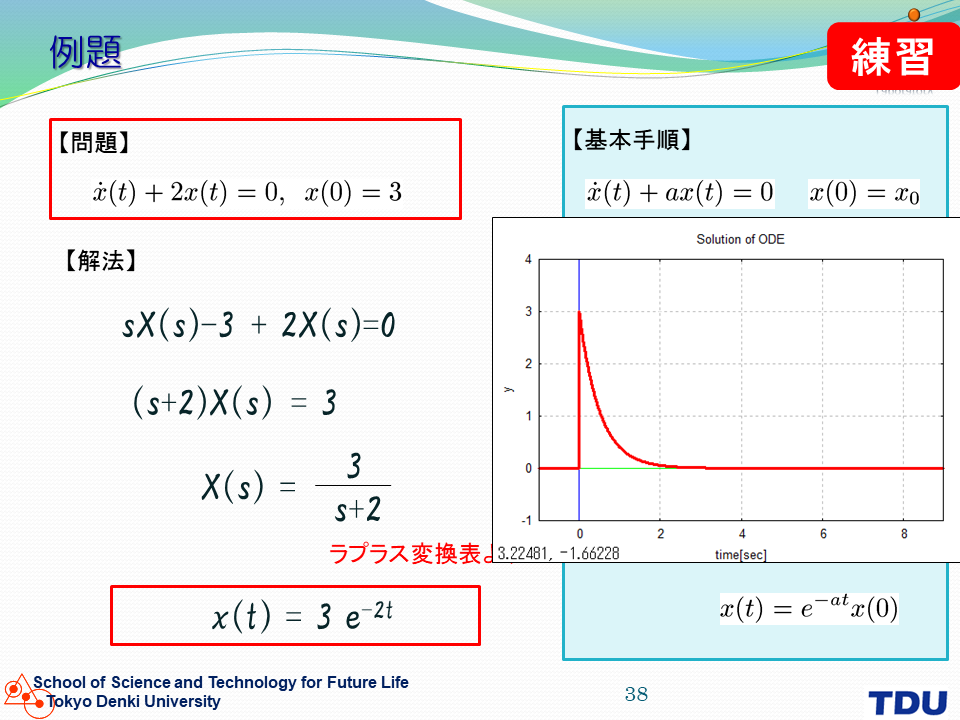
ラプラス変換を使って微分方程式を解く。 |
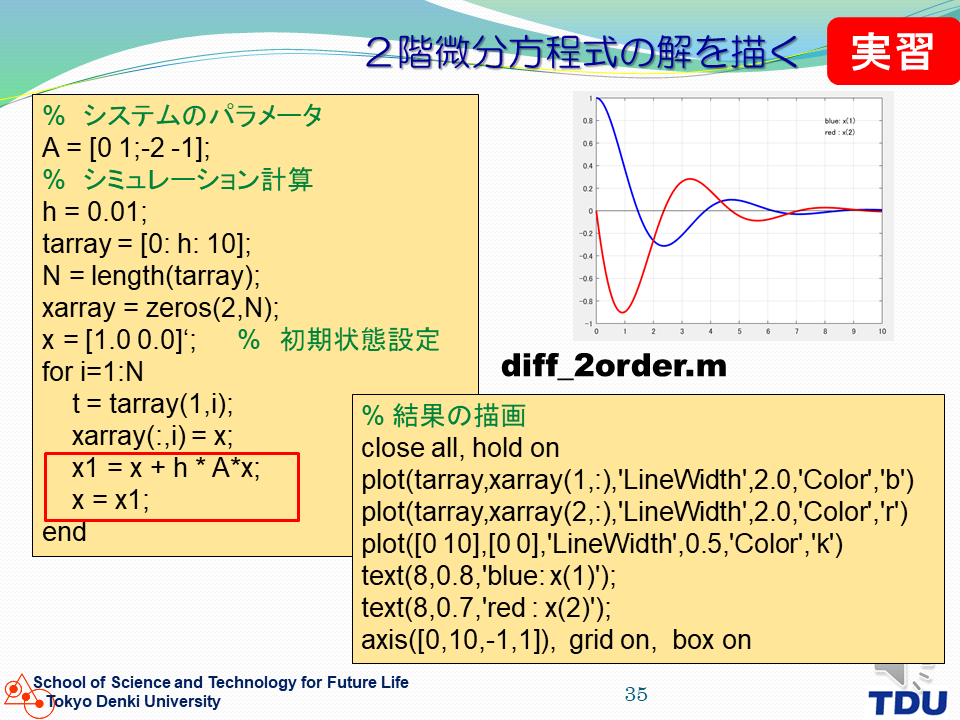
微分方程式の解をパソコンで計算して描画する。 |
 |
 |
|
角度1ラジアンの定義をもう一度確認しましょう。 |
数表とグラフと数式を自在に使いこなせることは語学としての数学の基本スキルです。 |
 |
 |
|
ネイピア数は制御工学や電気工学分野の大事な定数です。 |
オイラーの公式は古典制御理論において最も基本となる公式です。 |
 |
 |
|
虚数単位 j をかけることは90度の回転操作に対応します。 |
時間領域での微分演算操作は周波数領域でのsの乗算操作に対応する。 |
 |
 |
|
ラプラス変換を使って微分方程式を解く。 |
微分方程式の解をパソコンで計算して描画する。 |
資料請求
ロボット・メカトロニクス学科についてもっと知りたい!と思われた方は、
こちらから資料請求してください。お待ちしております!
ロボット・メカトロニクス学科についてもっと知りたい!と思われた方は、こちらから資料請求してください。お待ちしております!

ロボット・メカトロニクス学科
岩瀬研究室 | 汐月 哲夫 教授
ピタゴラスは「万物の根源は数である」と言い、ガリレオは「宇宙は数学という言葉で書かれている」という名言を残しています。つまり、自然を含む世界の理解のために数学は必須であり、自然科学を基に人工物を創造して社会に貢献する工学分野においても「数学」は基本的なリテラシーということなのです。言ってみれば「数学力」とは「語学力」のようなものなのです。単語を覚えるように定義を覚え、文法を理解するように公式や定理を理解し、会話や作文でコミュニケーション力を養うように演習問題やモデリングで数学を活用する力を修得します。語学に4つの目標、読む、書く、聞く、話すがあるように、数学にも、数学を使って考え、表現し、伝達し、議論するということが数学力があります。これらの能力をこの授業を通じて育てましょう。数学的思考スキルの面白さは厳密さと柔軟性が同居している点にあります。問題と解答の組合せを覚える受験数学から一日でも早く脱して、数学の持つ深い魅力を満喫してください。